PLO:学习笔记 | 零知识证明算法之PLONK——电路_区块链技术通俗讲解中山大学

最近研究了下零知识证明算法-PLONK。肚子里的墨水又增加了，记一下学习成果与新的体会，和大家共同学习---江小白。

现状

近些年，各种新的零知识证明算法层出不出，各有各的特点，各有各的优势。借用V神系列文章里的一张图来简单呈现下当前的零知识证明算法现状。

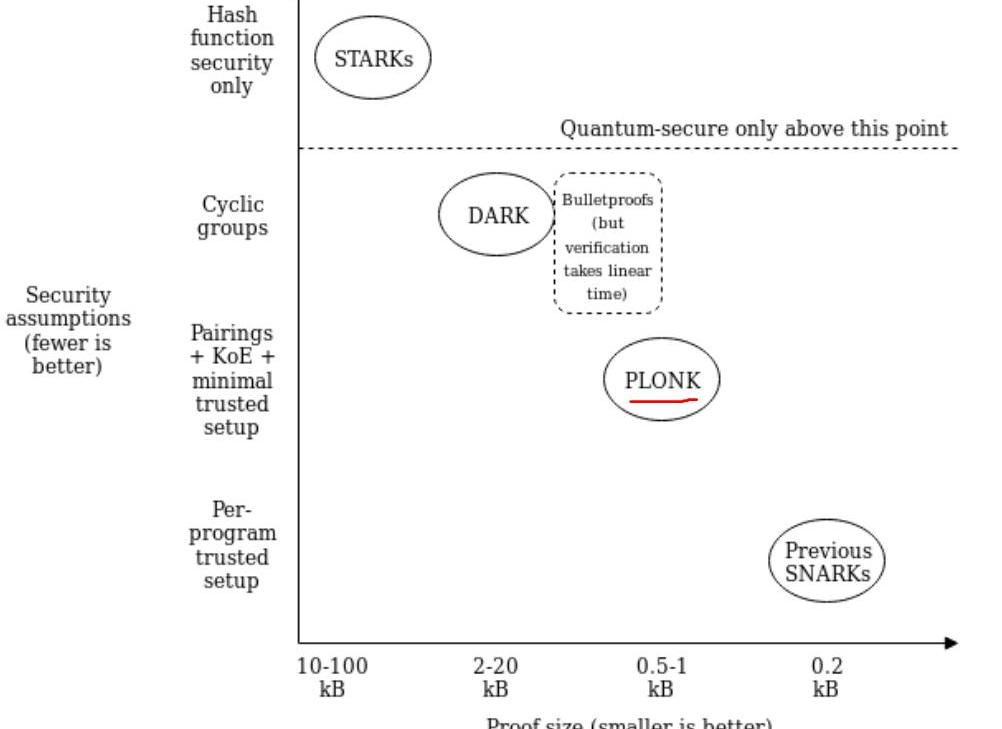
从图中可以简单总结出以下几点：

理论上安全性最高的是STARKs算法，不依赖数学难题假设，具有抗量子性；Proof大小上最小的是SNARKs算法，如Groth16;PLONK算法在安全性上和Proof大小上，位于上述两者之间；其他的这里不做过多阐述，如想了解零知识证明更多信息，可参考链接；对于SNARKs算法，绕不开的一个点就是中心化的TrustSetup，也称之为CRS(theCommonReferenceString)。而无论是PGHR13,Groth16,还是GM17算法，它们的CRS都是一次性的，不可更新的。即，不同的问题将对应着不同的CRS，这在某些场景下，会变得比较麻烦。这些存在的问题，变成了PLONK，SONIC这类算法的一个优势，它们算法虽然也需要中心化的可信设置，但是它的CRS具有一定的普适性。即，只要电路的大小不超过CRS的上限阈值，一些证明问题就可以共用一个CRS，这种CRS称之为SRS(universalStructuredReferenceString)，关于SRS的定义，详细的可参考SONIC协议里的第3小节。PLONK算法继用了SONIC算法的SRS的思想，但是在证明的效率上，做了很大的提升。接下来，让我们详细的介绍下PLONK算法的具体细节，主要从下面四个小节去分享：

微软Azure云机器学习设备群遭门罗币挖矿劫持:微软于6月10日表示，在其Azure云计算网络上一部分用于机器学习的设备群被黑客劫持用于 Monero（XMR）挖矿。微软通过分析数十个被攻击的设备群，发现黑客攻击的目标是开源平台Kubernetes的机器学习工具包 Kubeflow。

在默认情况下，只能从节点内部访问控制Kubeflow，因此，用户需要通过Kubernetes API使用端口进行访问。但是，部分用户修改了端口，将漏洞暴露在网上，从而导致设备被劫持。[2020/6/12]

电路的设计--描述PLONK算法的电路的描述思想；置换论证或者置换校验--复制约束，证明电路中门之间的一致性；多项式承诺--高效的证明多项式等式的成立；PLONK协议--PLONK协议剖析；电路

PLONK算法电路的描述和SONIC算法一直，具体的过程可以参考李星大牛的分享，已经写的比较详细且易懂。在这个小篇幅里，我想主要分享下我自己的两点想法：

声音 | 学习时报：纸质发票造假成灾 区块链发票是个好东西:学习时报发文表示，借助于区块链发票，税务机构便可自动封堵各种程序漏洞，同时湮灭各种非法违规行为，实现对国家税收的高效治理。一方面，根据分布式账本要求，区块链发票由税务机关、开票方、流转方、报销方多方参与共同记账，且共识机制确保了只有税务机关写出的发票才能得到校验与认可，其他任何节点写出的发票都不能得到确认，从而保证了发票源头的真实性；另一方面，借助区块链智能合约，交易与发票同时发生，消费支付与发票开具无缝进行，实物流与资金流、资金流与发票流做到二流合一，由此保证了发票的唯一性。这种全新的信用体系完全可以将一票多开、一票多用以及虚报虚抵的违规行为消弭于无形；不仅如此，区块链具有溯源性，区块链电子发票上的每一个干系人都能够追溯到发票真伪的来源，税务机关更可做到无界和跨界监控，这种发票信息的全场景透明完全可以使各种违法犯罪行为无法遁形。[2020/1/15]

无论是什么样的电路描述方式，电路的满足性问题都要归结于2点，门的约束关系和门之间的约束关系成立；在SNARKs系列的算法里，电路的描述单元都是以电路中有效的线为基本单元，具体的原理可以参考我之前分享的文章，而在PLONK，SONIC以及HALO算法里，电路的描述单元都是以门为基本单元。这两种电路的不同描述方式带来了一定的思考。那就是，之前在研究SNARKs算法时，我们都已经相信一个事实，“多项式等式成立，就代表着每个门的约束成立”，然后推断，整个电路逻辑都是成立；在这个过程中，并没有额外的去证明门之间的一致性成立；但是在PLONK算法里，除了要证明多项式等式成立外，还要额外的用置换论证的数学方法去证明门之间的约束关系，即复制约束。为何会有这样的区别？希望有心的读者能一起在评论区探讨这个问题？我个人理解是因为电路的描述方式的不同：

动态 | 越南公司与大学合作开发区块链普通话学习平台:据VietNamNews报道，越南创新区块链平台Beowulf最近宣布与国立师范大学（NTNU）建立合作关系，并将推出基于区块链的普通话远程教学平台Victoria，可帮助希望随时随地学习普通话的老师和学生建立联系。[2019/10/9]

PLONK算法里，电路描述的单元是门，它为每个门定义了自己的L,R,O，因此需要证明门之间的一致性；SNARKs算法里，电路描述的单元是线，门与门之间的值用的是同一个witness，因此不用额外证明一致性；置换论证

前面我们说过，在PLONK算法里，需要去证明门之间的约束关系成立。在做具体的原理解释之前，我们先简单的过一下PLONK协议的过程，如下图所示：

可描述为：

根据电路生成三个多项式，分别代表这电路的左输入，右输入，输出；利用置换校验协议，去证明复制约束关系成立；步骤3和4，校验门的约束关系成立。其中第1点已经在电路小节里阐述过了，接下来，将详细的讲解多项式置换校验的原理。先从简单的场景去讲解：

动态 | 济南市历下区领导干部大会：加强区块链等新知识学习:2月12日下午，济南市历下区召开全区领导干部大会。2019年，历下区将在学习和实践中不断汲取能量、提高本领。通过加强产业金融、人工智能、区块链等新理论、新知识的学习，着力增强专业思维、专业素养，努力做所在领域的专家、行家、实干家，在实践中增才干。[2019/2/14]

单个多项式的置换校验

其实就是证明对于某个多项式f，存在不同的两个点x,y，满足f(x)=f(y)。下面来看具体的原理：

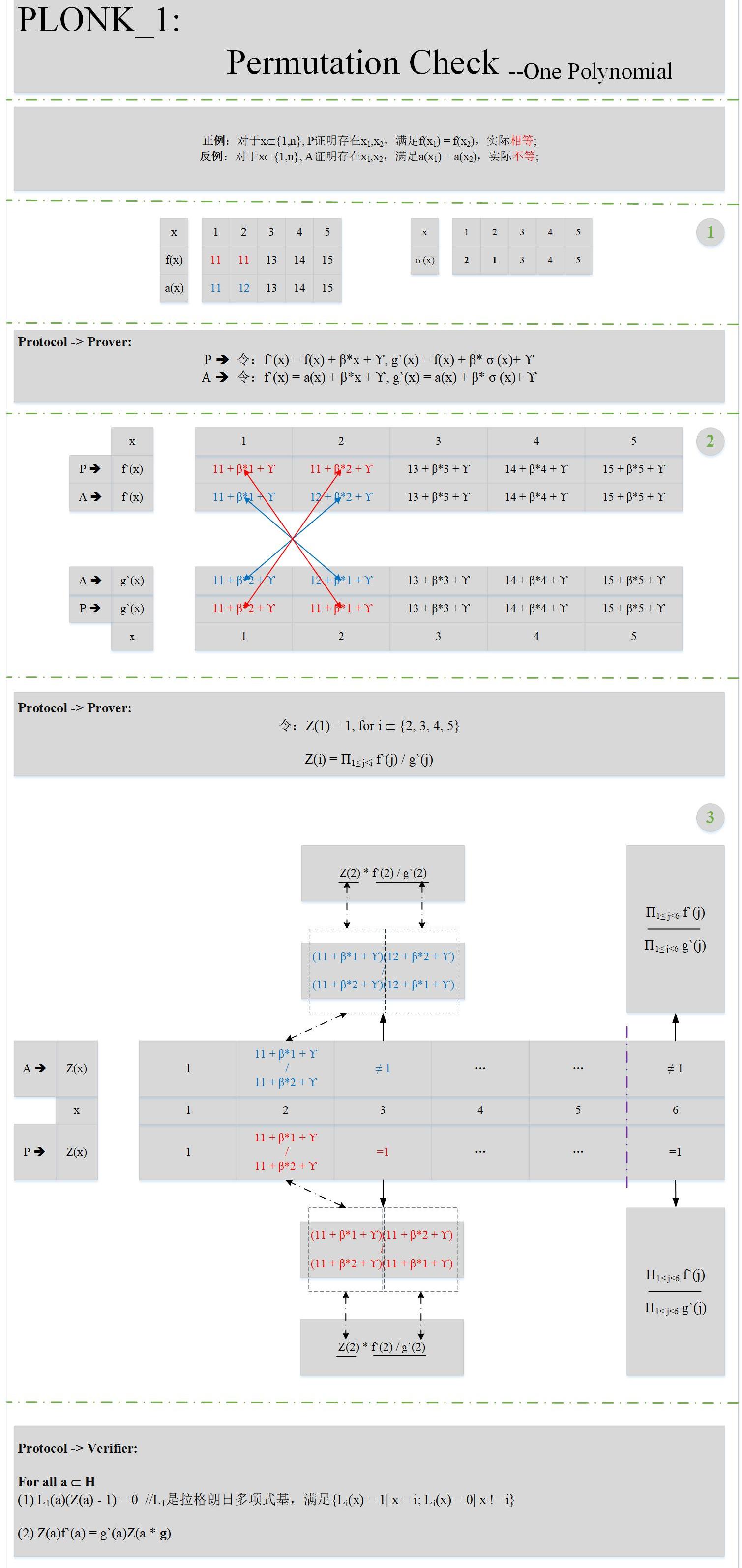
上图中加入了一个正例P，一个反例A，方便大家理解置换校验的原理。有几点需要解释的是：

而经过仔细剖析Z的形式，不难发现，Z(n+1)其实就是两个函数所有值的乘积的比值(不知是否等同于V神文章里的坐标累加器？)。理论上是等于1。因此，我们需要设计这样的一个多项式Z，需满足：deg(Z)<n

日本虚拟货币协会将召开虚拟货币会计处理等实务处理学习会:日本虚拟货币协会（JCBA）将在3月28日面向会员召开“基于资金结算法的虚拟货币会计处理等实务处理”学习会。[2018/3/21]

Z(n+1)=1

2.乘法循环群刚好可以满足这个条件，如果设计一个阶为n的一个乘法循环群H，根据群的性质可以知道Z(g)=Z(g^(n+1))。因此，在设计Z时，会保证Z(g)=1；上图中的自变量的取值也将从{1...n}变成{g...g^n}。所以在上图中验证的部分，a其实已经换成了群H里的所有元素。

3.根据论文中的协议，多项式Z是会发给可信第三方I验证方V会从I处获取到多项式Z在所有a处的取值，然后依次校验。

下面具体看一下论文中的定义：

从定义中可以看出：多项式f,g在范围内具有相同的值的集合；下面看一下论文中具体的协议部分，结合上述解释的3点：

说明：图4中的f,g对应图3中的f。即f,g是同一个多项式。其实只要是相同的值的集合，也可以不用于是同一个多项式。图3是一个特例而已。

跨多项式的校验

其实就是证明对于某个多项式f，g，存在两个点x,y，满足f(x)=g(y)。与存在两处不同：

多个多项式；不强制x,y的关系，即也可以等，也可以不等；有了(1)小节的基础，这次我们先看一下相关的定义：

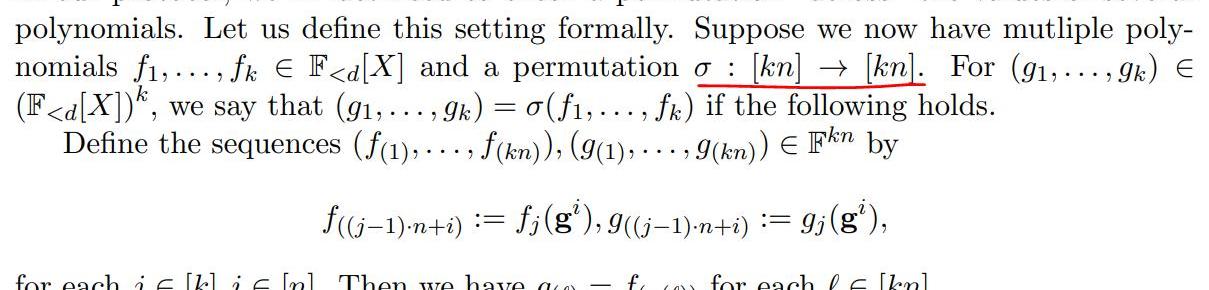
从定义可以看到，这次是两个多项式集合见的置换校验算法。从标注的部分可以看出：

两个多项式集合仍然具有相同的值的结合；为了区分集合里的多项式，自变量的索引得区分开来；因此，可以想象的到，如果存在两个多项式f,g，想要证明f(x)=g(y)，那么根据以上描述可以判断{f1,f2}={f,g}={g1,g2}。也保证了上述第1点的成立。

下面我们看一下具体的原理：

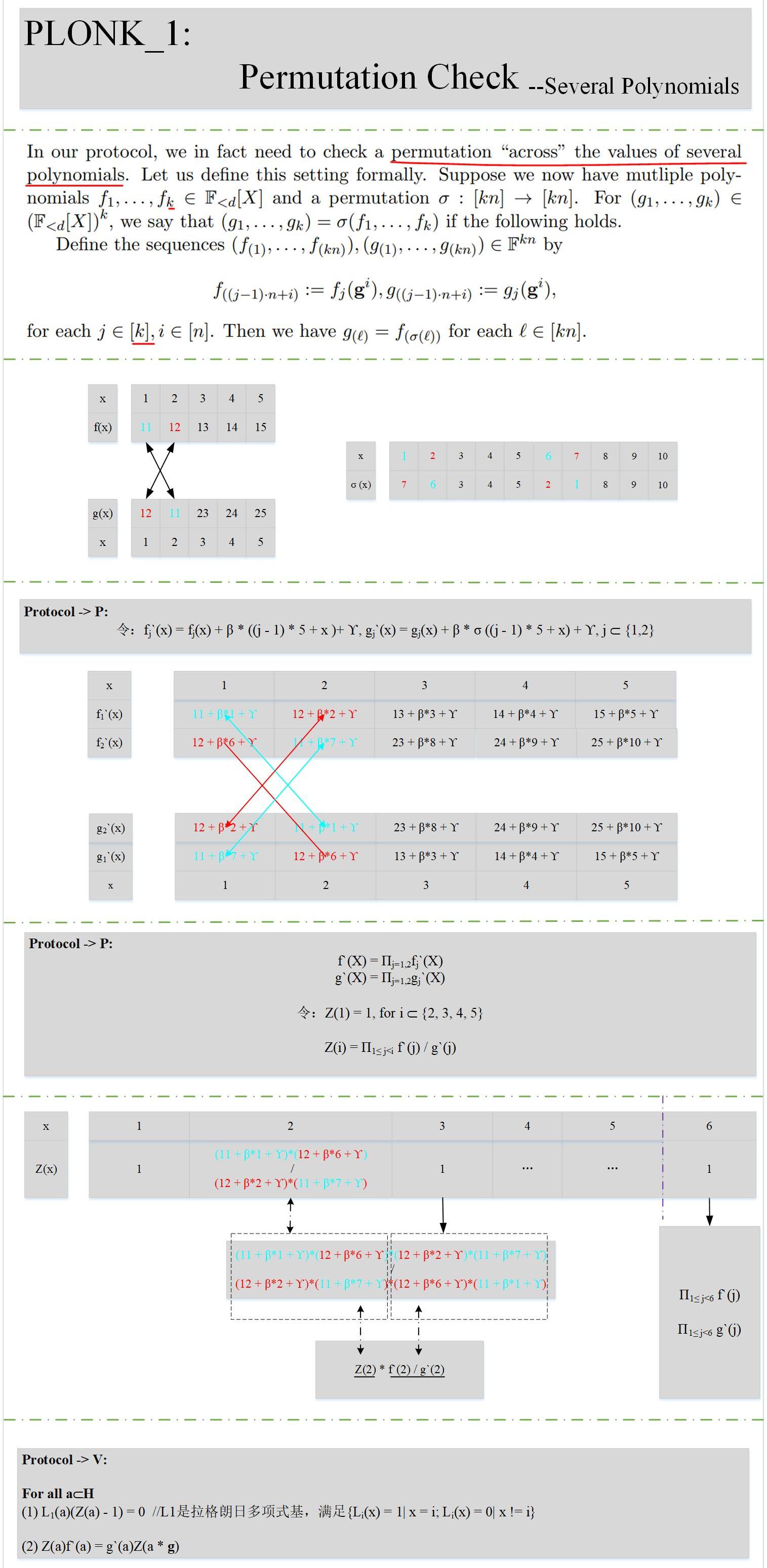
和(1)小节相比，证明方P增加了些工作量，验证方V工作量不变。结合上述描述，也能很容易的理解其数学原理。

说明：至此，其实我们已经慢慢的接触到PLONK算法的核心了，前面我们讲到，电路的满足性问题除了门的约束关系还有门之间的约束关系。

比如一个输入x，它既是一个乘法门的左输入，又是另外一个乘法门的右输入，这就需要去证明L(m)=R(n)，这就是跨多项式的置换校验。

下面再给出论文里的协议内容：

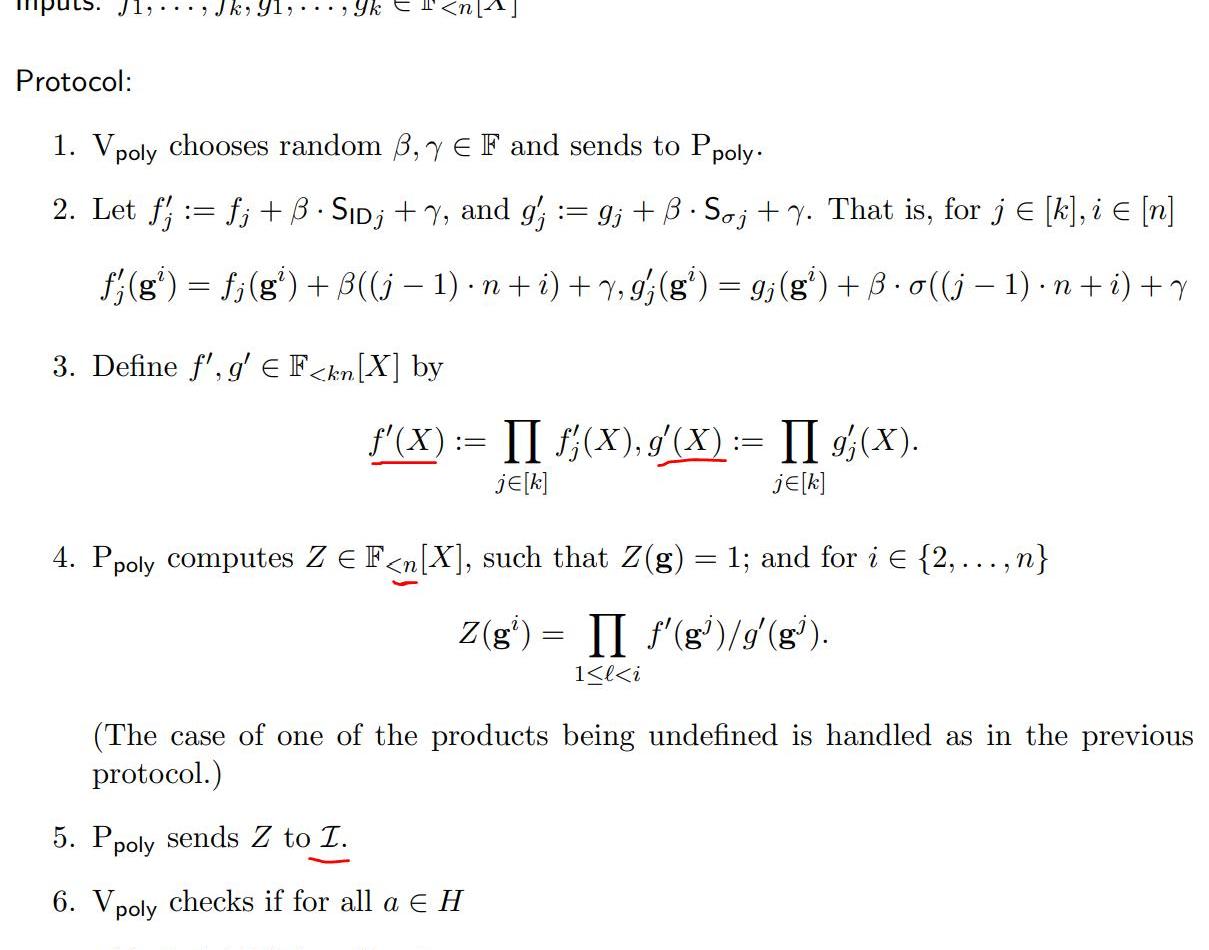
至此，本篇文章已经描述了，在PLONK算法里，电路的设计以及复制约束的成立验证两大部分，接下来，将会另起一片文章，去分享门约束的成立和整个协议的具体步骤。

以上都是作者小白的个人理解，还希望各位读者多多指教，谢谢。

标签：PLOLON区块链CRSPlow FinanceFC Barcelona Fan Token区块链技术通俗讲解中山大学crs币是什么意思

莱特币价格热门资讯