NFT:密码学研究 | 动手计算双线性对（上）_Xpansion Game

零知识证明是重要的密码学技术之一，其中基于电路的通用零知识证明算法更是因为近年取得的长足发展和在区块链项目中的应用而备受关注。双线性映射，也叫双线性配对或双线性对，是通用零知识证明算法的重要组成部分，也是众多密码体制，如聚合签名、身份基加密、属性基加密等的关键构件。本文从零基础开始，通过完整的模拟双线性对的原理来实现一套在小有限域上的双线性映射，帮助读者加深对双线性映射的理解。

“动手计算双线性对”这个系列计划有上中下三篇内容，本文是上篇，介绍后面文章需要的一些基础知识。在中篇，我们将对一个名为curve101的曲线进行讨论，其有限域只涉及101个元素，用于配对的椭圆曲线子群只有17个点，不借助计算机也能方便的通过纯手算完成整个过程，十分适合零基础读者入手。下篇则会实际计算并讨论双线性对的实际例子，全部的中间计算过程我们都将列出，读者可以按步骤重现整个计算流程。

在之后介绍零知识证明算法的系列文章中我们还会用到这个curve101进行演示，届时读者可以更加明白双线性对的作用，而接下来我们就来一起从零基础开始演算这个双线性曲线。

谷歌前CEO曾称赞比特币是一项卓越的密码学成就:金色财经报道，在最近被发现的一段旧视频中，谷歌前CEO Eric Schmidt称赞比特币是一项卓越的密码学成就。据悉，Schmidt是2014年在计算机历史博物馆中发表的这一看法。

他认为，比特币的技术很重要，但对该资产作为货币的用途表示怀疑。他表示，比特币的技术可以在未来为更多企业提供动力。（Finbold）[2022/8/7 12:07:20]

众所周知，很多公钥密码体制都是建立在有限域上，特别是模素数的有限域。作为零基础的系列，我们不去纠结数学概念“域”的严格定义，而是通过介绍带模运算相关的内容，来真实的展现一个有限域。

带模运算是在我们熟悉的加法和乘法的基础上增加一步计算余数的操作，例如，在以7为模数的系统中：

3+3=6，也就是mod7=6

3+6=2，也就是mod7=2

4×2=1，也就是mod7=1

《卫报》：部分密码学家对市场使用“Crypto”的方式感到不满:11月22日消息，据英国《卫报》报道，随着Crypto在加密货币行业使用越来越广泛，用户在 Google 上搜索“crypto”会看到大量指向比特币和以太坊等加密货币的热门搜索结果，但根据韦伯斯特字典对“crypto”的定义，它指的是密码学，而密码学又被定义为“信息的计算机编码和解码”。“这种词汇转变给密码学家带来了沉重的负担，”该报道称，过去几年许多密码学家一直在社交媒体上重复“crypto is cryptography”的口号，但收效甚微。密码学专家Matt Blaze表示，“我认为将加密货币称为 'crypto' 是一个糟糕的选择，这对密码学和加密货币都会产生不良后果。”[2021/11/22 22:08:04]

所谓模素数就是说取模操作针对的是某个素数p，例如上述的7，或者curve101中的101。p是素数这个细节是关键的，在下文介绍带模乘法的逆运算时你将会对这一点的必要性有更深的体会。

密码学家Matthew Green：端到端加密面临着越来越大的阻力:约翰·霍普金斯大学密码学家、安全技术专家和计算机科学教授Matthew Green表示，试图整合端到端加密的公司正面临着一场艰苦的战斗，因为开发保护私人通信系统的创新者面临着越来越大的阻力。Green表示：“真正让我担心的是，美国和其他政府强烈要求阻止部署新的E2E加密。”去年，美国总检察长William Barr与来自美国、英国和澳大利亚的国际执法合作伙伴签署了一封公开信，批评Facebook在其所有消息平台上实施E2E的计划，致使对端到端加密（E2E）的反击受到了很大推动。（The Daily Hodl）[2020/6/6]

有了模加法，我们可以定义其逆运算是模减法，例如：

6-3=3，也就是mod7=6

2-6=3，也就是mod7=3

同理，有了模乘法，自然而然会想到去定义其逆运算“模除法”。但是加、减、乘我们可以直接正向计算得到，“模除法”就比较困难。例如为了求3/2等于几必须思考哪个数乘以2等于3，而这个思考过程并不是特别直接。好在我们模7的例子中涉及到的元素并不多，因此通过穷举就能找到答案：因为2×5=3，所以3/2等于5。

声音 | 观点：密码学人才短缺，影响了马来西亚的区块链发展:私人投资公司MW Partners Group Holdings Pte Ltd顾问Mark Pui表示，密码学领域的人才短缺，拖累了马来西亚数字账本技术的发展。

Mark声称：“我认为，现实是我们没有密码技术，这影响了我们领导区块链技术发展的能力。在马来西亚和全世界，区块链技术的应用仍然有限。但在发展方面，我们落后于其他所有人，因为我们没有技能，没有深厚的密码学技能。”（The Malaysian Reserve）[2019/11/29]

需要注意到3/2其实可以转化为3×(1/2)，而因为刚才我们计算过4×2=1，所以1/2的值我们其实是知道的。因此3/2=5可以通3×4=5计算出来。这启发我们可以枚举全部形如1/n的数得到一个“倒数表”，然后借助“倒数表”将除法转化为乘法进行。

声音 | 上海交通大学来学嘉：区块链为密码学创造了价值:据巴比特消息，上海交通大学教授来学嘉在接受采访时提到了区块链对密码学的两大贡献。第一大贡献是为抗抵赖、抗捏造提供了完整的解决方案。区块链能做到抗抵赖，是因为区块链本身就是第三方，参与者自觉服从，数字签名为抗抵赖提供证据。另外，他还指出了区块链对密码学的另一个贡献——区块链为密码学创造了价值，过去的密码学是“赔钱”的，因为要用于保护信息系统的安全，增加了开销；有了区块链后，现在的密码学是“值钱”的，因为密码算法的计算结果（coin）具有价值，另外算法本身也具有价值，比如勒索软件，你要付钱才能解开。[2019/2/25]

模7逆元表

按习惯，我们一般不用1/n的写法，也不用“倒数”这个称呼。而是将1/n写做?n-1，并将其称为n的逆元。下文我们将遵从习惯，使用逆元这个叫法。显而易见的是，在不同的模系统中，同一个数的逆元是不同的。比如模7系统中，3的逆元是5；而模11系统中3的逆元是4。因此除非有明确的语境和上下文，否则为了避免歧义，还要说明逆元是模几的逆元才有意义，比如一个完整的说法是：3的模7逆元是5。

在模7的系统中，我们为每个元素都找到了逆元，在模17和模101的系统中也可以完成这样的操作。那么我们自然而然会想：是否在任何模的情况下都能为每个元素找到逆元呢？答案是否定的，例如在模8的系统中，找不到任何一个数乘以2等于1，也就是说在模8的系统中计算1/2这个“除法”是没有意义的。实际上，只有在模为素数的情况下才能为每个元素都找到逆元，也就是说在模素数的情况下我们才可以给任意两个元素计算“除法”。在这样的模素数系统中，任意两个元素都能完成加减乘除四则运算，我们称模7加法、模7乘法和集合{0,1,2,3,4,5,6}组成一个有限域：模7剩余类域。

所谓“有限”的意思就是集合的元素是有限的，比如这里的7个元素。虽然在本篇科普性质的文章对待数学概念都并非十分严格和谨慎，但是这里仍然能够揭示域的一些关键性质。比如我们发现仅利用集合中的元素就能够计算四则运算。模7剩余类域是这样，有理数域、复数域等也都是这样，意识到这一点就已经足够完成后面文章的阅读了。我们后面用Fp代指模p剩余类域，例如F7，F101等。

讨论完了加减乘除四则运算，按照我们曾经学习有理数的思路，我们来考虑开平方运算。例如3×3mod7=2，所以3是2的“平方根”。如果某个非零元素是可以开平方根的，我们称这样的元素为模7的二次剩余，否则就叫模7的二次非剩余。这样我们可以列出下面一张表：

可以注意到，二次剩余的个数和二次非剩余的个数是相等的，二次剩余的逆元仍然是二次剩余，二次非剩余的逆元也仍然是二次非剩余；而且我们还注意到，每个二次剩余都有两个根并且他们的和为0，这一点性质像极了正实数：正实数的平方根总有两个，他们互为相反数。

如何判定一个数是否为二次剩余和如何求二次剩余都是有趣和实用的问题。比如在动手计算双线性对会谈到的椭圆曲线中，已知x坐标和椭圆曲线方程求y的过程就需要考虑计算二次剩余的问题。相关的方法一般会涉及到勒让德符号等。而在我们的讨论的例子中因为元素的数量很少，我们一般采用穷举的方法就能解决。

经过上面的演算，我们发现3在F7中没有“平方根”，也就是不存在某个数其平方模7为3。类比复数域对实数域的扩展，我们假设3的一个平方根为j，即j*jmod7=3。现在我们把j加入到{0,1,2,3,4,5,6}集合中，然后尝试再加入一些其他元素使得新的集合仍然构成一个域。

首先为了能够计算加法和减法，至少还要加入j、1+j、2+j、3+j、4+j、5+j、6+j，为了能够计算乘法我们至少还要加入j、2j、3j、4j、6j、6j，最终我们发现一个新的能够计算四则运算的集合至少要有下面49个元素：

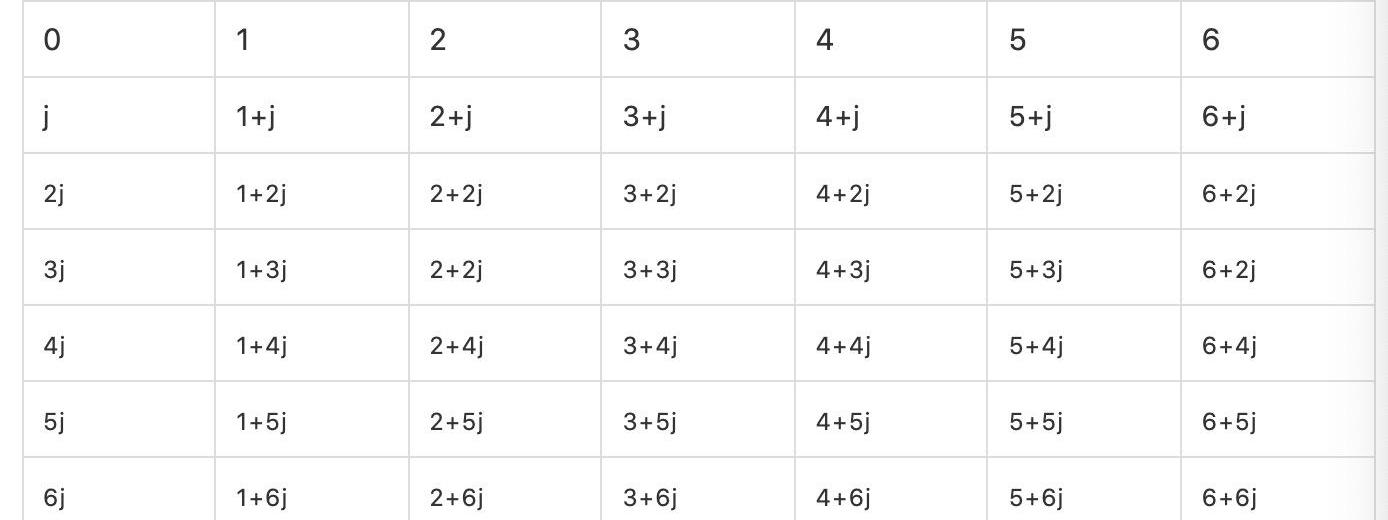
例如6j+j=0；(3+j)(5+2j)=4j;(4+4j)-1=6-6j

那么仅用这49个元素能够完成四则运算吗？答案是肯定的，虽然本文不去严格证明这一点，但是可以简单揭示一些其中的原因：

对于加法和减法，我们很容易验证任意两个元素的和、差都在还在集合中；对于乘法，因为j×j=3这条规则，简单验证后我们就能发现任何两个元素的积还是在集合中；唯一需要仔细考虑一下的是除法；对于除法，我们总可以通过如下方式计算a+bj的逆元：

因为a和b是F7中的元素，因此a2-3b2?也是F7中的元素，因此可以判定a2-3b2?的逆元仍然是{0,1,2,3,4,5,6}中的元素。所以最后可以发现a+bj的逆元是(a-bj)(a2-3b2)-1，它仍然落在49个元素之中。所以新的49个元素组成的集合不但包含{0,1,2,3,4,5,6,j}，而且能够计算四则运算。这个新的集合其实也是一个有限域，我们称其为F7的二次扩域，记为F72，之所以是“二次”，我们可以这样粗暴的理解：每个F72中的元素需要两个F7的元素通过组合的方式来表示。

本篇介完了关于模运算和模p剩余类域的一些基础知识，下一篇“动手计算双线性对”，我们会介绍关于有限域上椭圆曲线的一些例子和知识，届时会使用到本篇中的内容，敬请期待。

作者简介

乔沛杨趣链科技基础平台部区块链底层密码学小组

标签：NFT区块链GAMEGAMCOLLECTIVE Vault (NFTX)为什么要有区块链BIT Game TokenXpansion Game

比特币行情热门资讯